Have you ever looked at a math problem with lots of different signs – plus, minus, times, and brackets – and wondered where to even begin? It’s a common puzzler, that. Well, the good news is that there’s a set of agreed-upon rules, a sort of roadmap, to help us all get to the same correct answer every single time. These rules are what we call the order of operations, and they are pretty important for keeping things consistent in the world of numbers.
You see, without a standard way to work through these problems, things would get quite messy, very quickly. Imagine if everyone solved the same equation in their own unique way; we'd end up with all sorts of different results, and that would be a real problem for math, wouldn't it? This is precisely why we have rules like BODMAS and PEMDAS, which are essentially memory aids to help us remember the correct sequence for doing mathematical tasks. They make sure that when you tackle a problem, you’re following the same steps as everyone else, which is really quite clever.
Now, you might have heard of BODMAS, or perhaps PEMDAS, or maybe even both. It's almost like they are two sides of the same coin, yet they have slightly different names, which can be a little confusing for people just starting out or even for those who have been away from math for a while. The core idea behind them is identical, but the terms used are different, and that, in a way, is what we are going to explore today. We’ll look at what each one means, how they work, and if they always lead to the same answer, so you can feel more confident with your calculations.
Table of Contents
- Understanding the Order of Operations
- What is BODMAS?
- What is PEMDAS?
- The Main Difference: BODMAS vs PEMDAS
- Why These Rules Are So Important
- BODMAS, PEMDAS, and Computer Programming
- Common Questions About BODMAS and PEMDAS
- Wrapping Up Your Math Journey
Understanding the Order of Operations
So, what exactly are these "operations" we keep talking about? Well, in math, operations are the actions you perform on numbers. Think of things like adding them together, taking one away from another, multiplying them, dividing them, or even raising them to a power, like squaring a number. If it’s not a number itself, it's probably an operation, that's a pretty good way to think about it. The order of operations is simply a collection of agreed-upon rules that tell us which of these actions to do first when we have a problem with more than one of them. It's a standard convention, you know, something everyone agrees on to keep things tidy and consistent.
This idea of a set order is not just for school math problems; it is actually a fundamental part of how mathematics works and how computer programs understand equations. If you didn't have this order, imagine the chaos! You could get many different answers for the same problem, and that would be, well, a bit of a disaster for math. For example, if you have 2 + 3 × 4, if you add first, you get 5 × 4 = 20. But if you multiply first, you get 2 + 12 = 14. Which one is right? The order of operations tells us the second one is correct, so that's pretty useful.
The rules are there to prevent this kind of confusion, to make sure everyone arrives at the same answer. It's like a universal language for solving math problems. My text mentions that without these rules, you could "prove some unequal numbers like 1=2," which really highlights how essential they are for maintaining the very fabric of mathematical truth. So, these rules are not just some arbitrary things teachers make you learn; they are actually quite foundational to how numbers behave, and that's a pretty big deal.
What is BODMAS?
BODMAS is a very popular acronym, especially in countries like the UK and Australia, that helps people remember the correct sequence of mathematical operations. It stands for ‘Brackets, Orders, Division, Multiplication, Addition, Subtraction’. It's a simple way to keep the steps straight in your head, so you can tackle those tricky math expressions. My text explains that BODMAS is "an acronym used in mathematics to represent the order of operations," which is a pretty clear way to put it.
To use BODMAS, you start at the beginning of the word and work your way through. You always handle the things inside brackets first, then any powers or roots, then division and multiplication (working from left to right), and finally, addition and subtraction (also from left to right). This methodical approach helps you break down a big, scary problem into smaller, more manageable pieces. It’s a good system, really, for making sure you don't miss a step or do things out of order.
Brackets First
The 'B' in BODMAS stands for Brackets. This means that any calculation inside parentheses, square brackets, or curly braces should be done first, no matter what other operations are present. Think of brackets as shouting, "Do me first!" For instance, if you have 5 × (2 + 3), you would first work out what's inside the brackets, which is 2 + 3 = 5. Then, you would multiply 5 by 5 to get 25. It's a pretty straightforward rule, and it helps to simplify the problem right from the start, you know.
It's like setting aside a small part of the problem to solve completely before you bring its result back into the larger equation. This is a very, very important first step because getting the value inside the brackets wrong will throw off your entire answer. My text mentions, "To use BODMAS, start by working out the calculations in the brackets," which pretty much sums up this initial phase of the process. It's a solid way to begin.
Orders or Indices
Next up is 'O' for Orders, which some people also call Indices or Exponents. This refers to numbers that have been raised to a power, like 2 squared (2²) or 3 cubed (3³), or even square roots. After you've sorted out everything inside the brackets, your next task is to deal with these powers or roots. So, if you have something like 4 + 2³, you'd first calculate 2³, which is 2 × 2 × 2 = 8. Then you'd add 4 to 8 to get 12. It's a pretty clear step, really, and it comes right after those bracket calculations.
This step is about simplifying any numbers that have these special mathematical "orders" attached to them. It ensures that the value of these powered numbers is correctly established before you move on to the more common operations. It's a bit like preparing your ingredients before you start cooking; you want all your numbers to be in their simplest form before you begin the main arithmetic, so that's quite helpful.
Division and Multiplication
The 'D' and 'M' in BODMAS stand for Division and Multiplication. These two operations are actually on the same level of priority. This means that once you've handled brackets and orders, you perform any division or multiplication you see, working from left to right across the expression. It's not that division always comes before multiplication, or vice versa; they are equal partners, so you just do whichever one appears first as you read the problem from left to right.
For example, in a problem like 10 ÷ 2 × 3, you would first do the division: 10 ÷ 2 = 5. Then, you would take that result and multiply it by 3: 5 × 3 = 15. If it were 10 × 2 ÷ 4, you'd do the multiplication first: 10 × 2 = 20, then the division: 20 ÷ 4 = 5. My text notes, "division and multiplication (from left to right)," which is a very important detail to remember for this step. It's a common place where people can get a little mixed up.
Addition and Subtraction
Finally, we have 'A' for Addition and 'S' for Subtraction. Just like division and multiplication, these two operations are also on the same level of priority. This means that after you've taken care of brackets, orders, and all the division and multiplication, you then perform any addition or subtraction, again working from left to right across the expression. It's the last set of operations you perform, bringing everything together for your final answer.
So, if you have 15 - 5 + 2, you would first do the subtraction: 15 - 5 = 10. Then, you would add 2 to that result: 10 + 2 = 12. If it were 5 + 15 - 2, you'd do the addition first: 5 + 15 = 20, then the subtraction: 20 - 2 = 18. This left-to-right rule is really key for these last steps too. It helps ensure consistency, and that's a pretty big deal for getting the right answer every time.
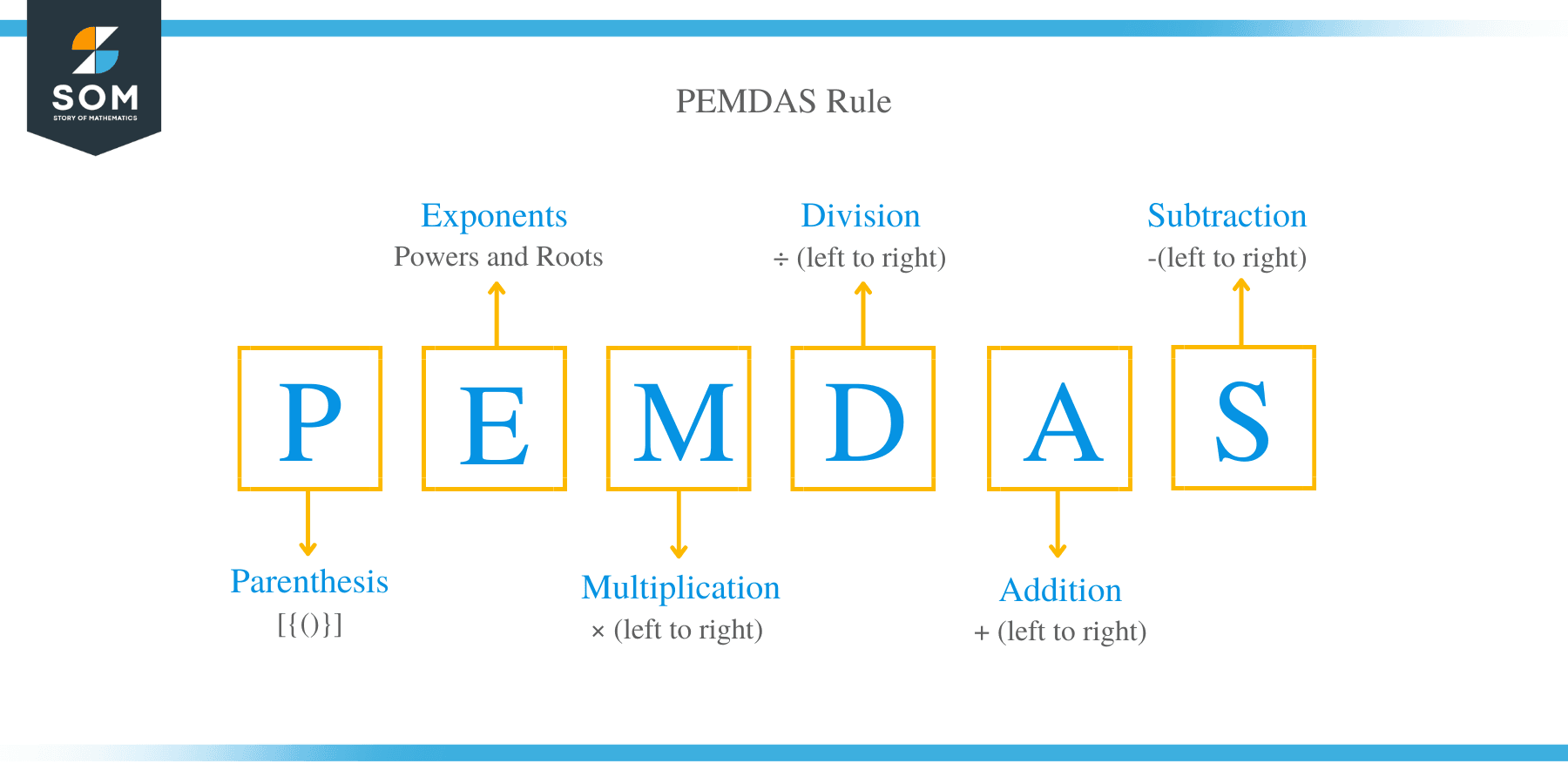
What is PEMDAS?
PEMDAS is another widely used acronym for the order of operations, particularly common in the United States. It stands for 'Parentheses, Exponents, Multiplication, Division, Addition, Subtraction'. As my text points out, "Pemdas parentheses > exponents > multiplication > division > addition > subtraction." You might notice it's very, very similar to BODMAS, just with slightly different words for some of the letters. The underlying logic and the sequence of operations are virtually identical.
Just like with BODMAS, you tackle problems by following the letters of PEMDAS in order. You always start with what's inside parentheses, then handle any exponents, then multiplication and division (from left to right), and finally, addition and subtraction (also from left to right). It's a systematic approach that helps keep your calculations organized and accurate. It's quite effective, really, for breaking down complex problems.
Parentheses: The Start
The 'P' in PEMDAS stands for Parentheses. This is the exact same concept as 'Brackets' in BODMAS. It means you must complete any calculations enclosed within these curved symbols first. For example, in an expression like 6 ÷ (1 + 2), you would first compute the sum inside the parentheses: 1 + 2 = 3. After that, you would proceed with the division: 6 ÷ 3 = 2. It's a very clear first step, and it sets the stage for the rest of the calculation.
This initial step is crucial because it simplifies a part of the problem before you apply other operations. It ensures that the result of the parenthetical expression is fully determined before it interacts with the rest of the numbers. So, in a way, it helps to keep things neat and manageable, which is pretty helpful when you're faced with a long string of numbers and operations.
Exponents: Next Up
The 'E' in PEMDAS refers to Exponents. This is the same idea as 'Orders' or 'Indices' in BODMAS. It covers numbers raised to a power (like 5² or 7³) and also includes roots (like square roots or cube roots). Once you've dealt with everything inside the parentheses, your next step is to evaluate any exponents present in the expression. So, if you see something like 10 - 3², you would first calculate 3², which is 3 × 3 = 9. Then, you would perform the subtraction: 10 - 9 = 1.
This step is all about making sure that any numbers with powers are fully calculated and turned into a single value before you move on to multiplication or division. It's a necessary step to simplify the expression further. It's quite important, actually, to get these values right early on, so they don't cause issues later in the calculation.
Multiplication and Division (PEMDAS)
The 'M' and 'D' in PEMDAS stand for Multiplication and Division. Just like in BODMAS, these two operations hold equal importance. You perform them from left to right as they appear in the expression, after you've handled parentheses and exponents. It's not a case of multiplication always coming before division; you just do whichever one shows up first when you're reading the problem from left to right.
Consider an example like 24 ÷ 4 × 2. You would first perform the division: 24 ÷ 4 = 6. Then, you would take that result and multiply it by 2: 6 × 2 = 12. If the problem were 24 × 4 ÷ 2, you would first do the multiplication: 24 × 4 = 96. Then, you would divide that by 2: 96 ÷ 2 = 48. This left-to-right rule for multiplication and division is really a key part of the process, and it helps keep things consistent, which is quite nice.
Addition and Subtraction (PEMDAS)
Finally, the 'A' and 'S' in PEMDAS represent Addition and Subtraction. These are the last operations you perform, and they are also on the same level of priority. Once you've completed all the parentheses, exponents, multiplication, and division, you then carry out any addition or subtraction, working from left to right across the expression. This is where you bring all the simplified parts of the problem together for the final answer.
For example, if you have 8 + 6 - 3, you would first do the addition: 8 + 6 = 14. Then, you would subtract 3 from that result: 14 - 3 = 11. If the problem were 8 - 6 + 3, you would first do the subtraction: 8 - 6 = 2. Then, you would add 3 to that: 2 + 3 = 5. This consistent left-to-right approach for addition and subtraction is pretty important for getting the correct final sum or difference.
The Main Difference: BODMAS vs PEMDAS
At first glance, BODMAS and PEMDAS seem almost identical, and in many ways, they are. The core sequence of operations is the same: tackle the innermost parts first, then powers, then multiplication/division, and finally addition/subtraction. My text clearly states, "The term bodmas is an acronym used to remember the order of operations to be followed when solving arithmetic expressions involving multiple operations," and it mentions PEMDAS as an alternative.
The most obvious difference is in the terminology. BODMAS uses 'Brackets' and 'Orders', while PEMDAS uses 'Parentheses' and 'Exponents'. These are just different words for the same mathematical concepts, so there's no real operational difference there. Brackets and parentheses both mean "do this part first." Orders and exponents both mean "handle powers or roots." So, in that sense, they lead to the same result.
However, the phrasing of "My text" also highlights a subtle point of discussion: "The difference is in the order of execution of division and multiplication." This statement, while perhaps intending to clarify, can sometimes cause confusion. It's important to remember that both BODMAS and PEMDAS treat multiplication and division as having equal priority. You always perform them from left to right as they appear in the equation. The same goes for addition and subtraction; they also have equal priority and are done from left to right.
So, it's not that 'D' always comes before 'M' in BODMAS, or 'M' always before 'D' in PEMDAS. It's about their grouping. They are often grouped together as (D/M) and (A/S) to show they are done in order of appearance from left to right. This is a crucial detail. If you have 10 ÷ 5 × 2, both rules say to do the division first (10 ÷ 5 = 2), then the multiplication (2 × 2 = 4). If it were 10 × 5 ÷ 2, both say to do the multiplication first (10 × 5 = 50), then the division (50 ÷ 2 = 25). So, in practice, they yield the same results because the underlying rule for equal-priority operations is consistent.
The confusion mentioned in my text about "the difference is in the order of execution of division and multiplication" often arises when people misinterpret the acronyms as strict sequential lists rather than hierarchical levels. It's a common misunderstanding, but ultimately, if applied correctly with the left-to-right rule for operations of the same level, both BODMAS and PEMDAS will always give you the same correct answer for any given mathematical expression. They are just different ways to say the same thing, a bit like saying "lift"